Y nuestro octavo y último invitado de los chicos de la RedLBC es Michael Morales (@mikael_mm en Twitter) que nos envió esta entrada de su blog Saltos Convergentes como regalo para el Cumpleaños de Star Tres. Esperamos que la disfruten 🙂 .
Estrellas, conos y bastones, y el cómo vemos: de Hiparco a logarítmos, y la Ley Fechner-Weber
De pequeño uno de los datos que quedaron grabados en mi mente en relación a la vista fue el de los conos y bastones. Años después, en libros de astronomía, uno es introducido a la historia y definición de magnitudes estelares. ¿Cómo relacionamos algo de lo que se sabe de la vista con las estrellas? Se sabe y dice que la visión humana es logarítmica, y no es sorpresa que las magnitudes estelares esten descritas a su vez por un logarítmo. Acá se hará la simple conexión entre ambas ideas a la vez de repasar algunas definiciones e introducir algunos conceptos.
Tenemos que ir en orden y empezamos con las magnitudes estelares. Recordemos que no se busca dar todo un curso de astronomía, sino cubrir las generalidades, especialmente si ya hay blogs más especializados en cubrir a detalle dichos tópicos.
Magnitudes estelares
Hiparco (190BC-120BC) definió una escala de magnitudes para referirse al brillo de estrellas. Esta escala era completamente subjetiva y tenía seis categorías de 1, muy brillante, a 6, muy débil (apenas perceptible). En esa época era mucho pedir el uso de decimales en la comparación.
Norman Pogson, en 1956, nota que la relación de brillos entre una estrella de magnitud 1 era 100 veces más brillante que una estrella de magnitud 6 (cinco unidades de diferencia), utilizando un modelo logarítmico para su descripción. Por alguna razón no es común encontrar su nombre acompañando la conocida ecuación de magnitudes. Si se tienen dos estrellas, una de magnitud y otra de magnitud
, con los brillos
y
, respectivamente, tenemos que la razón de brillos está dada por la expresión:
la cual puede reescribirse para tener la diferencia de magnitudes
Generalidades del cómo vemos
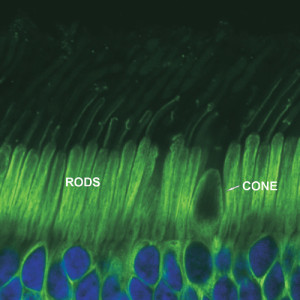 Pues, el sistema del ojo es complejo en sí, pero en la parte básica de cómo percibimos la luz están involucrados dos juegos de células ubicadas en la retina: conos y bastones. La retina es la responsable de comunicar la información del nervio óptico al cerebro.
Pues, el sistema del ojo es complejo en sí, pero en la parte básica de cómo percibimos la luz están involucrados dos juegos de células ubicadas en la retina: conos y bastones. La retina es la responsable de comunicar la información del nervio óptico al cerebro.
Los Bastones: son muy sensibles y son importantes para condiciones pobres de luz, es decir, la obscuridad; unos 92 millones de células de este tipo. Son monocromáticos.
Los Conos: son poco sensibles, pero son los responsables de percibir la luz de día, los colores; unos 4.6 millones de ellos. Hay de tres tipos para este fin, uno para cada color: rojo, azul y verde (el RGB).
En 1834, el fisiólogo alemán Ernst Weber y el psicólogo experimental Gustav Fechner describieron la ley del estímulo. Esta ley indica que la sensación del cambio en un estímulo, , es proporcional al logarítmo del cambio del estímulo,
, en sí,
. Escrito de otra manera:
que equivale a
donde es una constante. Esta ley se aplica tanto a la audición como a la vista.
¿Cómo se relaciona la Ley de Fechner-Weber con la ecuación de Pogson de magnitudes de las estrellas?
Notemos que el cambio en el estímulo no es más que la diferencia de magnitudes, ya que esta fue una definición por su percepción subjetiva,
. Continuando con el abuso de los diferenciales, podemos escribir el cambio del estímulo como
. ¿Cuáles son los estímulos? Los brillos
y
. Combinando resultados obtenemos
por lo cual , al escribirlo en base logarítmica (10), equivale a
, y así tenemos la conexión entre la ecuación de Pogson de magnitudes estelares y la Ley Fechner-Weber.
Referencias:
- Carroll, B. y Ostile, D. (2007) “Introduction to modern astrophysics” Segunda edición. Addison-Wesley.
- Curcio, C., Sloan, K., Kalina, R., y Hendrickson, A. “Human Photoreceptor Tomography” J. of comp. neurology 292:497-523 (1990).
- Girod, B. “Human visual perception” (Lecture notes, Image and video compression)
- Pillow, J. “Methods and introduction to vision” (Lecture notes, Perception)
- Shen, J. “On the foundations of vision modeling I. Weber’s law and Weberized TV restoration”. Physica D 175 (2003) 241-251




Deja un comentario